如图所示，在光滑的水平面上有一质量为m，长度为l的小车，小车左端有一质量也是m可视为质点的物块．车子的右壁固定有一个处于锁定状态的压缩轻弹簧(弹簧长度与车长相比可忽略)，物块与小车间动摩擦因数为m，整个系统处于静止．现在给物块一个水平向右的初速度v0，物块刚好能与小车右壁的弹簧接触，此时弹簧锁定瞬间解除，当物块再回到左端时，与小车相对静止．求：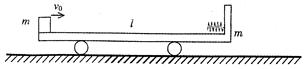
（1）物块的初速度v0．
（2）弹簧的弹性势能Ep
如图，传送带AB总长为l=10cm，与一个半径为R=0.4m的光滑四分之一圆轨道BC相切于B点，传送带速度恒为v=6m/s，方向向右，现有一个滑块以一定初速度
从A点水平滑上传送带，滑块质量为m=10kg，滑块与传送带间的动摩擦因数为μ=0.1，已知滑块运动到B端时，刚好与传送带同速，求：
（1）滑块的初速度，
（2）滑块能上升的最大高度h；
（3）求滑块第二次子啊传送带上滑行时，滑块和传送带系统产生的内能
如图所示，一物体M从A点以某一初速度沿倾角α=37°的粗糙固定斜面向上运动，自顶端B点飞出后，垂直撞到高H=2.25m的竖直墙面上C点，又沿原轨迹返回，已知B.C两点的高度差h=0.45m，物体M与斜面间的动摩擦因数μ=0.25，sin37°=0.6，cos37°=0.8，重力加速度取
，求：
（1）物体M沿斜面向上运动时的加速度大小
（2）物体返回B点时的速度
（3）物体被墙面弹回后，从B点回到A点所需时间
一长为L的细线，上端固定，下端栓一质量为m、带电荷量为q的小球，处于如图所示的水平向右的匀强电场中，开始时，将线与小球拉成水平，然后释放，小球由静止开始向下摆动，当细线转过60°角时，小球到达B点速度恰好为零，求：
（1）AB两点的电势差
（2）匀强电场的场强大小
（3）小球到达B点时，细线对小球的拉力大小
在游乐场中，有一种大型游戏机叫“跳楼机”参加游戏的游客被安全带固定在座椅上，由电动机将座椅沿光滑的竖直轨道提升到离地面40m处，然后由静止释放，为研究方便，可以认为座椅沿轨道做自由落体运动1.2s后，开始受到恒定阻力而立即做匀减速运动，且下落到离地面4m高处时速度刚好减小到零，然后再让座椅以相当缓慢的速度稳稳下落，将游客送回地面，取
，求
（1）座椅在自由下落结束时刻的速度
（2）座椅在匀减速阶段的时间
（3）在匀减速阶段，座椅对游客的作用力大小是游客体重的多少倍
如图所示，AB.CD均是固定在同一竖直平面内的四分之一光滑圆弧轨道，圆轨道半径均为R=0.800m，下端点B.C间距L=0.900m，与紧靠的水平传送带上表面处于同一高度，传送带沿逆时针方向的传动速度恒为v=1.00m/s，一质量m=1.00kg的小物块从圆弧顶点A由静止开始沿轨道下滑，若物块与传送带之间的动摩擦因数μ=0.0200，不计物块经过轨道与传送带连接处B.C时的机械能损失，取
，试求：
（1）物块第一次沿CD轨道上山的最大高度
（2）物块从开始运动到第21次返回AB轨道的过程中，在传送带上运动的时间
（3）物块从第21次至第101次返回AB轨道的过程中，与传送带间摩擦产生的热量
粤公网安备 44130202000953号