如图所示,一底面粗糙、质量为m、倾角为30°的劈形物块放在粗糙的水平地面上,劈形物块的斜面为光滑面,现用一端固定的轻绳系一质量也为m的小球置于斜面上静止,轻绳与斜面的夹角也是30°,求:系统静止时,轻绳的拉力有多大?
若地面对劈形物的最大摩擦力为正压力的k倍,要使系统静止,k值必须符合什么条件。
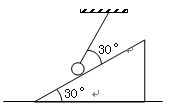
如图所示,一底面粗糙、质量为m、倾角为30°的劈形物块放在粗糙的水平地面上,劈形物块的斜面为光滑面,现用一端固定的轻绳系一质量也为m的小球置于斜面上静止,轻绳与斜面的夹角也是30°,求:系统静止时,轻绳的拉力有多大?
若地面对劈形物的最大摩擦力为正压力的k倍,要使系统静止,k值必须符合什么条件。
