如图所示,虚线MO与水平线PQ相交于O,二者夹角θ=30°,在MO左侧存在电场强度为E、方向竖直向下的匀强电场,MO右侧某个区域存在磁感应强度为B、垂直纸面向里的匀强磁场,O点处在磁场的边界上.现有一群质量为m、电量为+q的带电粒子在纸面内以速度v(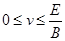 )垂直于MO从O点射入磁场,所有粒子通过直线MO时,速度方向均平行于PQ向左.不计粒子的重力和粒子间的相互作用力,求:
)垂直于MO从O点射入磁场,所有粒子通过直线MO时,速度方向均平行于PQ向左.不计粒子的重力和粒子间的相互作用力,求: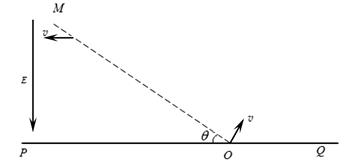
速度最大的粒子自O点射入磁场至返回水平线POQ所用的时间.
磁场区域的最小面积.
如图所示,虚线MO与水平线PQ相交于O,二者夹角θ=30°,在MO左侧存在电场强度为E、方向竖直向下的匀强电场,MO右侧某个区域存在磁感应强度为B、垂直纸面向里的匀强磁场,O点处在磁场的边界上.现有一群质量为m、电量为+q的带电粒子在纸面内以速度v(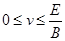 )垂直于MO从O点射入磁场,所有粒子通过直线MO时,速度方向均平行于PQ向左.不计粒子的重力和粒子间的相互作用力,求:
)垂直于MO从O点射入磁场,所有粒子通过直线MO时,速度方向均平行于PQ向左.不计粒子的重力和粒子间的相互作用力,求:
速度最大的粒子自O点射入磁场至返回水平线POQ所用的时间.
磁场区域的最小面积.