如图所示,MN、PQ是平行金属板,板长为L,两板间距离为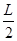 ,PQ板带正电,MN板带负电,在PQ板的上方有垂直纸面向里的匀强磁场。一个电荷量为q、质量为m的带负电粒子以速度
,PQ板带正电,MN板带负电,在PQ板的上方有垂直纸面向里的匀强磁场。一个电荷量为q、质量为m的带负电粒子以速度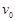 从MN板边缘沿平行于板的方向射入两板间,结果粒子恰好从PQ板左边缘飞进磁场,然后又恰好从PQ板的右边缘飞进电场。不计粒子重力。求:
从MN板边缘沿平行于板的方向射入两板间,结果粒子恰好从PQ板左边缘飞进磁场,然后又恰好从PQ板的右边缘飞进电场。不计粒子重力。求: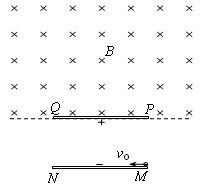
两金属板间所加电场的场强E大小
匀强磁场的磁感应强度B的大小
如图所示,MN、PQ是平行金属板,板长为L,两板间距离为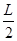 ,PQ板带正电,MN板带负电,在PQ板的上方有垂直纸面向里的匀强磁场。一个电荷量为q、质量为m的带负电粒子以速度
,PQ板带正电,MN板带负电,在PQ板的上方有垂直纸面向里的匀强磁场。一个电荷量为q、质量为m的带负电粒子以速度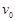 从MN板边缘沿平行于板的方向射入两板间,结果粒子恰好从PQ板左边缘飞进磁场,然后又恰好从PQ板的右边缘飞进电场。不计粒子重力。求:
从MN板边缘沿平行于板的方向射入两板间,结果粒子恰好从PQ板左边缘飞进磁场,然后又恰好从PQ板的右边缘飞进电场。不计粒子重力。求:
两金属板间所加电场的场强E大小
匀强磁场的磁感应强度B的大小