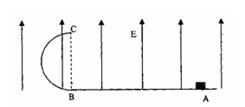
如图所示，竖直放置的半圆形绝缘轨道半径为R，下端与光滑绝缘水平面平滑连接，整个装置处于方向竖直向上的匀强电场E中。一质量为m、带电量为+q的物块（可视为质点），从水平面上的A点以初速度v₀水平向左运动，沿半圆形轨道恰好通过最高点C，场强大小为E（E小于mg/q）。
试计算物块在运动过程中克服摩擦力做的功。
证明物块离开轨道落回水平面时的水平距离与场强大小E无关，且为一常量。