如图所示，在光滑的水平面上，有两个质量都是M的小车A和B，两车间用轻质弹簧相连，它们以共同的速度向右运动，另有一质量也为M的粘性物体，从高h处自由下落，正好落至A车并与之粘合在一起，在此后的过程中，弹簧获得最大弹性势能为E。
求：A、B车开始匀速运动的初速度V0的大小？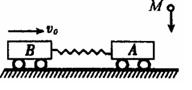
相关试题
如图所示，在光滑的水平面上，有两个质量都是M的小车A和B，两车间用轻质弹簧相连，它们以共同的速度向右运动，另有一质量也为M的粘性物体，从高h处自由下落，正好落至A车并与之粘合在一起，在此后的过程中，弹簧获得最大弹性势能为E。
求：A、B车开始匀速运动的初速度V0的大小？
,把
放在相距较远的两点，他们间作用力的大小为F，若使两球相接触后再分开放回原位置，求它们间作用力的大小．
C，
，让两绝缘金属小球接触，在接触的过程中，电子如何转移并转移了多少？
粤公网安备 44130202000953号