如左图所示，一足够长的固定斜面的倾角为q＝37°，物体与斜面间的动摩擦因数为m＝0.25，物体受到平行于斜面的力F作用，由静止开始运动。力F随时间t变化规律如右图所示（以平行于斜面向上为正方向，g＝10m/s2，sin37°＝0.6，cos37°＝0.8），求：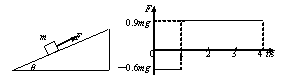
第1s和第2s内物体运动的加速度大小a1和a2；
前4s内物体的位移大小s。
如图甲所示的电路中，R1、R2均为定值电阻，且R1＝100 Ω，R2阻值未知，R3为一滑动变阻器．当其滑片P从左端滑至右端时，测得电源的路端电压随电源中流过的电流变化图线如图乙所示，其中A、B两点是滑片P在变阻器的两个不同端点得到的．求：
电源的电动势和内阻.
定值电阻R2的阻值．
滑动变阻器的最大阻值．
如图所示，在两根劲度系数都为k的相同的轻质弹簧下悬挂有一根导体棒ab，导体棒置于水平方向的匀强磁场中，且与磁场垂直.磁场方向垂直纸面向里，当导体棒中通以自左向右的恒定电流时，两弹簧各伸长了Δl1；若只将电流反向而保持其他条件不变，则两弹簧各伸长了Δl2，求：
导体棒通电后受到的磁场力的大小?
若导体棒中无电流，则每根弹簧的伸长量为多少?
如图所示，电源电动势E＝6V，电源内阻不计．定值电阻R1=2.4kΩ、R2=4.8kΩ.
若在ab之间接一个C=100μF的电容器，闭合开关S，电路稳定后，求电容器上所带的电量；
若在ab之间接一个内阻RV = 4.8kΩ的电压表，求电压表的示数．
质谱分析技术已广泛应用于各前沿科学领域。汤姆孙发现电子的质谱装置示意如图，M、N为两块水平放置的平行金属极板，板长为L，板右端到屏的距离为D，且D远大于L，O’O为垂直于屏的中心轴线，不计离子重力和离子在板间偏离O’O的距离．以屏中心O为原点建立xOy直角坐标系，其中x轴沿水平方向，y轴沿竖直方向．设一个质量为m0、电荷量为q0的正离子以速度v0沿O’O的方向从O’点射入，板间不加电场和磁场时，离子打在屏上O点．若在两极板间加一沿+y方向场强为E的匀强电场，求离子射到屏上时偏离O点的距离y0；
假设你利用该装置探究未知离子，试依照以下实验结果计算未知离子的质量数．
上述装置中，保留原电场，再在板间加沿-y方向的匀强磁场．现有电荷量相同的两种正离子组成的离子流，仍从O’点沿O’O方向射入，屏上出现两条亮线．在两线上取y坐标相同的两个光点，对应的x坐标分别为3.24mm和3.00mm，其中x坐标大的光点是碳12离子击中屏产生的，另一光点是未知离子产生的．尽管入射离子速度不完全相同，但入射速度都很大，且在板间运动时O’O方向的分速度总是远大于x方向和y方向的分速度（本题中洛伦兹力可近似看成恒力）．
粤公网安备 44130202000953号