如图所示，一带电量为2.0×10＝9C , 质量为1.8×10 –16Kg的粒子,在直线上一点O沿30o角方向进入磁感应强度为B的匀强磁场中,经历1.5×10- 6s后到达直线上另一点P.(重力不计)求：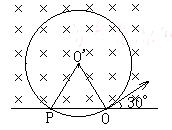
粒子作圆周运动的周期；
磁感应强度B的大小；
若OP距离为0.1m，则粒子的运动速度多大？
如图，一固定的斜面，其倾角为θ=30º，另一边与水平地面垂直，顶端有一定滑轮，跨过定滑轮的细线两端分别与物块A、B相连，A的质量为4m，B的质量为m。开始时，将B按在地上不动，然后放手，让A沿斜面下滑而B上升，所有摩擦均忽略不计。当A下滑距离为S时，细线突然断了。求B上升的最大高度。（设B不会与定滑轮相碰）
的固定斜面的
点水平抛出，初动能为
，落到斜面上的
点时，其动能是多少？
如图所示，斜面足够长，其倾角为α，质量为m的滑块，距挡板P为s0，以初速度v0沿斜面上滑，滑块与斜面间的动摩擦因数为μ，滑块所受摩擦力小于滑块沿斜面方向的重力分力，若滑块每次与挡板相碰均无机械能损失(即速度大小不变方向相反)，求滑块在斜面上经过的总路程为多少？ 
如图（甲）所示，
、
为平行放置的水平金属轨道，
、
为相同半径，平行放置的竖直半圆形金属轨道,
为切点，P、Q为半圆轨道的最高点，轨道间距
，圆轨道半径
，整个装置左端接有阻值
的定值电阻。M1M2N2N1、M3M4N4N3为等大的长方形区域Ⅰ、Ⅱ，两区域宽度
，两区域之间的距离
；区域Ⅰ内分布着均匀的变化的磁场B1，变化规律如图（乙）所示，规定竖直向上为B1的正方向；区域Ⅱ内分布着匀强磁场B2，方向竖直向上。两磁场间的轨道与导体棒CD间的动摩擦因数为
，
右侧的直轨道及半圆形轨道均光滑。质量
，电阻
的导体棒CD在垂直于棒的水平恒力F拉动下，从
处由静止开始运动，到达处撤去恒力F，CD棒可匀速地穿过匀强磁场区，并能通过半圆形轨道的最高点PQ处，最后下落在轨道上的位置离
的距离
。若轨道电阻、空气阻力不计，运动过程导棒与轨道接触良好且始终与轨道垂直，g取10 m/s2
求：
（1）水平恒力F的大小；
（2）CD棒在直轨道上运动过程中电阻R上产生的热量Q；
（3）磁感应强度B2的大小。
的圆形范围内，水面上的运动员手到脚的长度
.若已知水的折射率
，运动员的实际身高
，请计算该游泳池的水深H。
粤公网安备 44130202000953号