如图所示，电源的电动势E=110V，电阻R1=21Ω，电动机线圈的电阻R0=0.5Ω，电键S1始终闭合。当电键S2断开时，电阻R1的电功率是525W；当电键S2闭合时，电阻R1的电功率是336W，求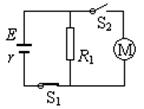
电源的内电阻；
当电键S2闭合时流过电源的电流和电动机的输出功率。
如图，与水平面成角的平面
将空间分成I和II两个区域。一质量为
、电荷量为
（q＞0）的粒子以速度
从平面
上的
点水平右射入I区。粒子在I区运动时，只受到大小不变、方向竖直向下的电场作用，电场强度大小为
；在II区运动时，只受到匀强磁场的作用，磁感应强度大小为
，方向垂直于纸面向里。求粒子首次从II区离开时到出发点
的距离。(粒子的重力可以忽略)
。
如图，两根足够长的金属导轨、
竖直放置，导轨间距离为
电阻不计。在导轨上端并接两个额定功率均为
、电阻均为
的小灯泡。整个系统置于匀强磁场中，磁感应强度方向与导轨所在平面垂直。现将一质量为
、电阻可以忽略的金属棒
从图示位置由静止开始释放。金属棒下落过程中保持水平，
且与导轨接触良好。已知某时刻后两灯泡保持正常发光。重力加速度为。求：
(1)磁感应强度的大小：
(2)灯泡正常发光时导体棒的运动速率。
如图所示。以、
和
、
为端点的两半圆形光滑轨道固定于竖直平面内，一滑板静止在光滑水平地面上。左端紧靠
点，上表面所在平面与两半圆分别相切于
、
。一物块被轻放在水平匀速运动的传送带上
点。运动到
时刚好与传送带速度相同，然后经
沿半圆轨道滑下。在经
滑上滑板。滑板运动到
时被牢固粘连。物块可视为质点。质量为
，滑板质量
,两半圆半径均为，
板长
，板右端到C的距离
在
范围内取值，
距
为
,物块与传送带、物块与滑板间的动摩擦因数均为
。重力加速度取
。
(1) 求物块滑到点的速度大小，
(2) 试讨论物块从滑上滑板到离开滑板右端的过程中．克服摩擦力做的功与
的关
系，并判断物块能否滑到轨道的中点．
如图（）所示，在以
为圆心，内外半径分别为
和
的圆环区域内，存在辐射状电场和垂直纸面的匀强磁场，内外圆间的电势差为
常量，
,一电荷量为
，质量为
的粒子从内圆上的
点进入该区域，不计重力。
(1)已知粒子从外圆上以速度射出，求粒子在
点的初速度
的大小
(2)若撤去电场，如图19（）,已知粒子从
延长线与外圆的交点
以速度
射出，方向与
延长线成45°角，求磁感应强度的大小及粒子在磁场中运动的时间
(3)在图（）中，若粒子从
点进入磁场，速度大小为
，方向不确定，要使粒子一定能够从外圆射出，磁感应强度应小于多少？
分布可简化为如图所示的折线，图中
粤公网安备 44130202000953号