如下图所示,两块竖直放置的平行金属板A、B,板距d=0.04m,两板间的电压U=400V,板间有一匀强电场,AB水平线上方场强可视为0。在A、B两板上端连线的中点Q的正上方,距Q为h=1.25m的P点处有一带正电小球,已知小球的质量m=5×10-6kg,电荷量q=5×10-8C。设A、B板长度足够长,(取g=10m/s2)。
试求:带正电小球从P点开始由静止下落,经多长时间和金属板相碰?
相碰时,离金属板上端的距离多大?
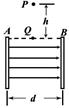
如下图所示,两块竖直放置的平行金属板A、B,板距d=0.04m,两板间的电压U=400V,板间有一匀强电场,AB水平线上方场强可视为0。在A、B两板上端连线的中点Q的正上方,距Q为h=1.25m的P点处有一带正电小球,已知小球的质量m=5×10-6kg,电荷量q=5×10-8C。设A、B板长度足够长,(取g=10m/s2)。
试求:带正电小球从P点开始由静止下落,经多长时间和金属板相碰?
相碰时,离金属板上端的距离多大?
