如右图所示,磁感应强度大小为B、方向垂直纸面向里的匀强磁场被约束在由边界ab、bc、cd形成的区域内(ab∥cd,bc⊥ab,ab和cd可以向右端无限延伸),一质量为m、电荷量为+q的带电粒子从bc边的中点O处,以大小为v的初速度垂直磁场方向射入此区域,初速度方向与bc边的夹角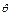 =30°.已知bc边的长度为L,粒子重力不计,试问:
=30°.已知bc边的长度为L,粒子重力不计,试问:
⑴若粒子最终能从边界ab射出,则初速度v应满足什么条件?
⑵粒子在匀强磁场中运动的最长时间应为多少?
如右图所示,磁感应强度大小为B、方向垂直纸面向里的匀强磁场被约束在由边界ab、bc、cd形成的区域内(ab∥cd,bc⊥ab,ab和cd可以向右端无限延伸),一质量为m、电荷量为+q的带电粒子从bc边的中点O处,以大小为v的初速度垂直磁场方向射入此区域,初速度方向与bc边的夹角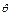 =30°.已知bc边的长度为L,粒子重力不计,试问:
=30°.已知bc边的长度为L,粒子重力不计,试问:
⑴若粒子最终能从边界ab射出,则初速度v应满足什么条件?
⑵粒子在匀强磁场中运动的最长时间应为多少?