如图所示是示波器的原理示意图.电子从灯丝发射出来,经电压为 的电场加速后,通过加速极板
的电场加速后,通过加速极板 上的小孔
上的小孔 射出,然后沿中心线
射出,然后沿中心线 进入
进入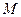 、
、 间的偏转电场,偏转电场的电压为
间的偏转电场,偏转电场的电压为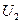 ,场强方向垂直于
,场强方向垂直于 ,电子离开偏转电场后,最终打在垂直于
,电子离开偏转电场后,最终打在垂直于 放置的荧光屏上的
放置的荧光屏上的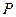 点.已知电子的电荷量为
点.已知电子的电荷量为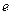 ,平行金属板
,平行金属板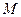 、
、 间的距离为
间的距离为 ,极板长为l,极板右端与荧光屏之间的距离为
,极板长为l,极板右端与荧光屏之间的距离为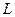 ,电子离开灯丝时的初速度可忽略,电子所受重力以及电子之间的相互作用力不计.
,电子离开灯丝时的初速度可忽略,电子所受重力以及电子之间的相互作用力不计.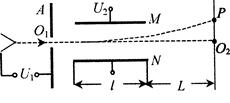
若把
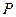 点到
点到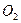 点的距离称为偏转距离Y,其偏转距离Y为多少?
点的距离称为偏转距离Y,其偏转距离Y为多少?求电子即将到达
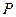 点时的动能.
点时的动能.
如图所示是示波器的原理示意图.电子从灯丝发射出来,经电压为 的电场加速后,通过加速极板
的电场加速后,通过加速极板 上的小孔
上的小孔 射出,然后沿中心线
射出,然后沿中心线 进入
进入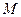 、
、 间的偏转电场,偏转电场的电压为
间的偏转电场,偏转电场的电压为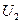 ,场强方向垂直于
,场强方向垂直于 ,电子离开偏转电场后,最终打在垂直于
,电子离开偏转电场后,最终打在垂直于 放置的荧光屏上的
放置的荧光屏上的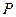 点.已知电子的电荷量为
点.已知电子的电荷量为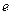 ,平行金属板
,平行金属板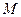 、
、 间的距离为
间的距离为 ,极板长为l,极板右端与荧光屏之间的距离为
,极板长为l,极板右端与荧光屏之间的距离为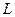 ,电子离开灯丝时的初速度可忽略,电子所受重力以及电子之间的相互作用力不计.
,电子离开灯丝时的初速度可忽略,电子所受重力以及电子之间的相互作用力不计.
若把
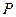 点到
点到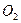 点的距离称为偏转距离Y,其偏转距离Y为多少?
点的距离称为偏转距离Y,其偏转距离Y为多少?求电子即将到达
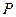 点时的动能.
点时的动能.