在真空中存在空间范围足够大的、水平向右的匀强电场.若将一个质量为m、带正电电量q的小球在此电场中由静止释放,小球将沿与竖直方向夹角为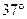 的直线运动。现将该小球从电场中某点以初速度
的直线运动。现将该小球从电场中某点以初速度 竖直向上抛出,求(取
竖直向上抛出,求(取
 )
)
小球受到的电场力的大小;
小球抛出点至最高点之间的电势差U.
在真空中存在空间范围足够大的、水平向右的匀强电场.若将一个质量为m、带正电电量q的小球在此电场中由静止释放,小球将沿与竖直方向夹角为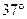 的直线运动。现将该小球从电场中某点以初速度
的直线运动。现将该小球从电场中某点以初速度 竖直向上抛出,求(取
竖直向上抛出,求(取
 )
)
小球受到的电场力的大小;
小球抛出点至最高点之间的电势差U.