如图所示,是示波器工作原理的示意图,电子经电压U1从静止加速后垂直进入偏转电场,偏转电场的电压为U2,两极板间距为d,极板长度为L,电子离开偏转电场时的偏转量为h,每单位电压引起的偏转量(h/U2)叫示波器的灵敏度,试求: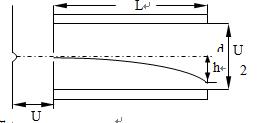
电子离开偏
 转电场时的偏转量h
转电场时的偏转量h该示波器的灵敏度h/U2
并探究可采用哪些方法提高示波器的灵敏度。
如图所示,是示波器工作原理的示意图,电子经电压U1从静止加速后垂直进入偏转电场,偏转电场的电压为U2,两极板间距为d,极板长度为L,电子离开偏转电场时的偏转量为h,每单位电压引起的偏转量(h/U2)叫示波器的灵敏度,试求:
电子离开偏
 转电场时的偏转量h
转电场时的偏转量h该示波器的灵敏度h/U2
并探究可采用哪些方法提高示波器的灵敏度。