在如图所示的电路中，R1是由某金属氧化物制成的导体棒，实验证明通过它的电流I和它两端的电压U遵循I＝kU3的规律(式中k＝0.02A/V3)，R2是普通电阻，阻值为24Ω，遵循欧姆定律，电源电动势E＝6V，闭合开关S后，电流表的示数为0.16A。试求：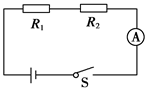
R1两端的电压；
电源的内电阻r；
R1上消耗的电功率P1。
在如图所示的装置中，电源电动势为E，内阻不计，定值电阻为R1，滑动变阻器总阻值为R2，置于真空中的平行板电容器水平放置，极板间距为d。处在电容器中的油滴A恰好静止不动，此时滑动变阻器的滑片P位于中点位置。
（1）求此时电容器两极板间的电压；
（2）求该油滴的电性以及油滴所带电荷量q与质量m的比值；
（3）现将滑动变阻器的滑片P由中点迅速向上滑到某位置，使电容器上的电荷量变化了Q1，油滴运动时间为t；再将滑片从该位置迅速向下滑动到另一位置，使电容器上的电荷量又变化了Q2，当油滴又运动了2t的时间，恰好回到原来的静止位置。设油滴在运动过程中未与极板接触，滑动变阻器滑动所用的时间与电容器充电、放电所用时间均忽略不计。求：Q1与Q2的比值。
如图所示，用长为l的绝缘细线拴一个质量为m、带电量为+q的小球（可视为质点）后悬挂于O点，整个装置处于水平向右的匀强电场中．将小球拉至使悬线呈水平的位置A后，由静止开始将小球释放，小球从A点开始向下摆动，当悬线转过
角到达位置B时，速度恰好为零．求：
（1）B、A两点的电势差UBA；
（2）电场强度E；
（3）小球到达B点时，悬线对小球的拉力T；
（4）小球从A运动到B点过程中的最大速度vm和悬线对小球的最大拉力Tm．
搭载有“勇气”号火星车的探测器成功登陆在火星表面 。“勇气”号离火星地面12m时与降落伞自动脱离，被众气囊包裹的“勇气”号下落到地面后又弹跳到15m高处，这样上下碰撞了若干次后，才静止在火星表面上。假设“勇气”号下落及反弹运动均沿竖直方向。已知火星的半径为地球半径的二分之一，质量为地球的九分之一（取地球表面的重力加速度为10m/s2）。
（1）根据上述数据，火星表面的重力加速度是多少？
（2）若被众气囊包裹的“勇气”号第一次碰火星地面时，其机械能损失为其12m高处与降落伞脱离时的机械能的20﹪，不计空气的阻力，求“勇气”号与降落伞脱离时的速度。
(16分)如图所示，内壁光滑的半径为R的圆形轨道，固定在竖直平面内，质量为m1小球静止在轨道最低点，另一质量为m2的小球（两小球均可视为质点）从内壁上与圆心O等高的位置由静止释放，到最低点时与m1发生弹性碰撞，求：
（1）小球m2运动到最低点时的速度大小；
（2）碰撞后，欲使m1能沿内壁运动到最高点，则m2/m1应满足什么条件？
的汽缸A、B竖直放置，底部用细管连通，气缸A中有定位卡环。现用质量分别为
="4.0" kg、
="2.0" kg的活塞封闭一定质量的某种理想气体，当气体温度为27℃时，活塞A恰与定位卡环接触，此时封闭气体的体积为
="300" mL，外界大气压强为
=1.0×105 Pa。（g取10m/s2）
粤公网安备 44130202000953号