均匀导线制成的单匝正方形闭合线框abcd,每边长为L,总电阻为R,总质量为m.将其置于磁感强度为B的水平匀强磁场上方h处,如图20所示.线框由静止自由下落,线框平面保持在竖直平面内,且cd边始终与水平的磁场边界面平行.当cd边刚进入磁场时:
(1)求线框中产生的感应电动势大小.
(2)求cd两点间的电势差大小.
(3)若此时线框加速度恰好为零,求线框下落的高度h所应满足的条件.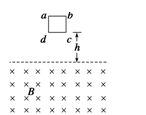
均匀导线制成的单匝正方形闭合线框abcd,每边长为L,总电阻为R,总质量为m.将其置于磁感强度为B的水平匀强磁场上方h处,如图20所示.线框由静止自由下落,线框平面保持在竖直平面内,且cd边始终与水平的磁场边界面平行.当cd边刚进入磁场时:
(1)求线框中产生的感应电动势大小.
(2)求cd两点间的电势差大小.
(3)若此时线框加速度恰好为零,求线框下落的高度h所应满足的条件.