在如图所示的电路中,R1、R2均为定值电阻,且R1=100Ω,R2阻值未知,R3是一滑动变阻器,当其滑片从左端滑至右端时,测得电源的路端电压随电流的变化图线如图所示,其中A、B两点是滑片在变阻器的两个不同端点得到的求: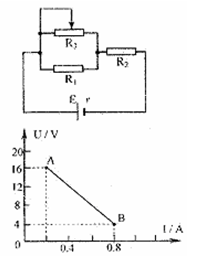
电源的电动势和内阻;
定值电阻R2的阻值;
滑动变阻器的最大阻值。
在如图所示的电路中,R1、R2均为定值电阻,且R1=100Ω,R2阻值未知,R3是一滑动变阻器,当其滑片从左端滑至右端时,测得电源的路端电压随电流的变化图线如图所示,其中A、B两点是滑片在变阻器的两个不同端点得到的求:
电源的电动势和内阻;
定值电阻R2的阻值;
滑动变阻器的最大阻值。