用一条绝缘细线悬挂一个带电小球，小球质量为m=1.0×10一2kg，
所带电荷量为q=+2.0×10一8C，现加一水平方向的匀强电场。平衡时
绝缘细线与竖直方向的夹角为θ=300。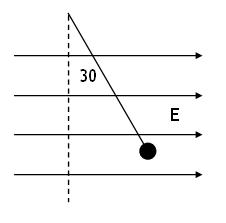
画出小球的受力示意图。
由平衡条件求出电场力的大小。
求匀强电场的电场强度E。
如图所示，PQ、MN两极板间存在匀强电场，MN极板右侧长、宽分别为2L、
的虚线区域内有垂直纸面的匀强磁场B。现有一初速度为零、带电量为q、质量为m的离子（不计重力）从PQ极板出发，经电场加速后，从MN上的小孔A垂直进入磁场区域，并从NF边界上某点垂直于虚线边界射出。求：
（1）匀强磁场的方向；
（2）PQ、MN两极板间电势差U；
（3）若带点粒子能从NF边界射出，则PQ、MN两极板间电势差的范围是多少？
如图所示，电源的电动势为50V，电源内阻为1.0
，定值电阻R=14，M为直流电动机，电枢电阻R′=2.0，电动机恰好正常运转，理想电压表读数为35V。求：
（1）在100s时间内电源做的功
（2）在100s时间内电动机转化为机械能的部分是多少
如图，在
的区域有垂直于纸面向里的匀强磁场，磁感应强度的大小为B，在x>a的区域有垂直于纸面向外的匀强磁场，磁感应强度的大小也为B。质量为m、电荷量为q（q>0）的粒子沿x轴从原点O射入磁场。（粒子重力忽略不计）
（1）若粒子以
的速度射入磁场，求其轨迹与x轴交点的横坐标
（2）为使粒子返回原点O，粒子的入射速度应为多大？
如图所示，固定的光滑金属导轨间距为L，导轨电阻不计，上端a、b间接有阻值为R的电阻，导轨平面与水平面的夹角为θ，且处在磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场中．质量为m、电阻为r的导体棒与固定弹簧相连后放在导轨上．初始时刻，弹簧恰处于自然长度，导体棒具有沿轨道向上的初速度v0.整个运动过程中导体棒始终与导轨垂直并保持良好接触．已知弹簧的劲度系数为k，弹簧的中心轴线与导轨平行．
（1）求初始时刻通过电阻R的电流I的大小和方向
（2）当导体棒第一次回到初始位置时，速度变为v，求此时导体棒的加速度大小a
（3）导体棒最终静止时弹簧的弹性势能为Ep，求导体棒从开始运动直到停止的过程中，电阻R上产生的焦耳热Q
粤公网安备 44130202000953号