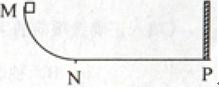如图,MNP为竖直面内一固定轨道,其圆弧段MN与水平段NP相切于N、P端固定一竖直挡板。M相对于N的高度为h,NP长度为s。一木块自M端从静止开始沿轨道下滑,与挡板发生一次完全弹性碰撞后停止在水平轨道上某处。若在MN段的摩擦可忽略不计,物块与NP段轨道间的滑动摩擦因数为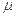 ,求物块停止的地方与N点距离的可能值。
,求物块停止的地方与N点距离的可能值。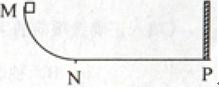
如图,MNP为竖直面内一固定轨道,其圆弧段MN与水平段NP相切于N、P端固定一竖直挡板。M相对于N的高度为h,NP长度为s。一木块自M端从静止开始沿轨道下滑,与挡板发生一次完全弹性碰撞后停止在水平轨道上某处。若在MN段的摩擦可忽略不计,物块与NP段轨道间的滑动摩擦因数为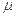 ,求物块停止的地方与N点距离的可能值。
,求物块停止的地方与N点距离的可能值。