发电机转子是100匝边长为20cm的正方形线圈,将它置于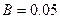 T的匀强磁场中,绕着垂直于磁场方向的轴以
T的匀强磁场中,绕着垂直于磁场方向的轴以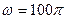 rad/s的角速度转动,转动开始时线圈平面与磁场方向垂直,已知线圈的电阻为2
rad/s的角速度转动,转动开始时线圈平面与磁场方向垂直,已知线圈的电阻为2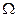 ,外电路的电阻为8
,外电路的电阻为8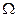 ,试求:
,试求:
(1)交变电流的瞬时表达式;
(2)如保持转子匀速转动,外力每分钟需要对转子所做的功;
(3)从计时开始,线圈转过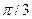 的过程中,通过外电阻的电量。
的过程中,通过外电阻的电量。
发电机转子是100匝边长为20cm的正方形线圈,将它置于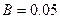 T的匀强磁场中,绕着垂直于磁场方向的轴以
T的匀强磁场中,绕着垂直于磁场方向的轴以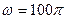 rad/s的角速度转动,转动开始时线圈平面与磁场方向垂直,已知线圈的电阻为2
rad/s的角速度转动,转动开始时线圈平面与磁场方向垂直,已知线圈的电阻为2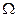 ,外电路的电阻为8
,外电路的电阻为8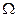 ,试求:
,试求:
(1)交变电流的瞬时表达式;
(2)如保持转子匀速转动,外力每分钟需要对转子所做的功;
(3)从计时开始,线圈转过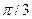 的过程中,通过外电阻的电量。
的过程中,通过外电阻的电量。