如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失)。已知圆弧半径R="0.3m" ,θ="60" 0,小球到达A点时的速度 vA="4" m/s 。(取g ="10" m/s2)求:
(1)小球做平抛运动的初速度v0;
(2)P点与A点的水平距离和竖直距离;
(3)小球到达圆弧最高点C时对轨道的压力。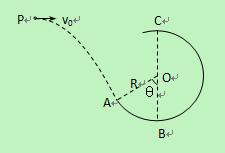
如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失)。已知圆弧半径R="0.3m" ,θ="60" 0,小球到达A点时的速度 vA="4" m/s 。(取g ="10" m/s2)求:
(1)小球做平抛运动的初速度v0;
(2)P点与A点的水平距离和竖直距离;
(3)小球到达圆弧最高点C时对轨道的压力。