如图所示，有一磁感强度B=2T的水平匀强磁场，垂直匀强磁场放置一很长的金属框架，框架上有一导体ab保持与框架边垂直、由静止开始下滑．已知ab长10cm，质量为0.1Kg，电阻为1Ω，框架电阻不计，取g=10m/s2．求：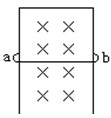
(1)导体ab下落的最大加速度和最大速度；
(2)导体ab在最大速度时产生的电功率．
相关试题
如图所示，AB是粗糙的
圆弧，半径为R，OA水平，OB竖直，O点离地面高度为2R，一质量为m的小球，从A点静止释放，不计空气阻力，最后落在距C点R处的D点。求：
（1）小球经过B点时，对轨道的压力大小。
（2）小球在AB段克服阻力做的功。
如图所示，质量为m的小球自由下落d后，沿竖直面内的固定轨道ABC运动，AB是半径为d的四分之一粗糙圆弧，BC是直径为d的光滑半圆弧，B是轨道的最低点，小球运动到C点对轨道的压力恰为零。求小球在AB圆弧上运动过程中，克服摩擦力做了多少功？
一颗人造地球卫星在绕地球做匀速圆周运动，卫星距地面的高度是地球半径的15倍，即h=15R，试计算此卫星的线速度大小。已知地球半径R=6400km，地球表面重力加速度g=10m/s2.
如图所示，飞行员的质量为m=60kg，重力加速度为g=10m/s2，他驾驶飞机在竖直平面内做翻筋斗的圆周运动，当飞机飞到最高点时速度为
，飞行员对机座的压力恰好为零，则轨道半径R= m，若飞机飞到最低点时速度为
，飞行员对机座的压力N= N。
，周期为
。已知万有引力常量为G。 
，周期为
，试估算该行星周围众多卫星的总质量。
粤公网安备 44130202000953号