如图，有理想边界的匀强磁场的磁感强度B＝10T，宽度d＝10cm，正方形单匝金属线框abcd边长l＝20cm，总电阻R＝0.5Ω，线框总质量M=1kg,若bc边保持与磁场边界平行，bc边刚进入磁场时向右的速度为v＝4m／s，ad边刚好离开磁场时向右的速度为v1＝1m／s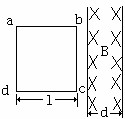
求：(1)当bc边进入磁场时，线框中电流的大小？
(2)线框从在bc边进入磁场到ad边刚好离开磁场的过程中，安培力对金属框所做的功？回路中产生的焦耳热？
如图所示，一电子束（电子电量为e）以水平速度υ垂直于磁感应强度为B的匀强磁场中（磁场方向垂直于纸面向里），穿过磁场时，电子水平位移为d，速度方向与进入磁场时的速度方向成30°角，则：
；
。
⑴电子的质量是多少？
⑵穿过磁场的时间是多少？
在可控核反应堆中需要给快中子减速，轻水、重水和石墨等常用作减速剂。中子在重水中可与
核碰撞减速，在石墨中与
核碰撞减速。上述碰撞可简化为弹性碰撞模型。某反应堆中快中子与静止的靶核发生对心正碰，通过计算说明，仅从一次碰撞考虑，用重水和石墨作减速剂，哪种减速效果更好？
如图所示，在坐标系的第一象限内有一横截面为四分之一圆周的柱状玻璃体OPQ，OP=OQ=R，一束单色光垂直OP面射入玻璃体，在OP面上的入射点为A，OA=
，此单色光通过玻璃体后沿BD方向射出，且与x轴交于D点，OD=
，求：
①该玻璃的折射率是多少？
②将OP面上的该单色光至少向上平移多少，它将不能从PQ面直接折射出来。
如图所示，第一象限的某个矩形区域内，有方向垂直于纸面向里的匀强磁场
，磁场的左边界与y轴重合，第二象限内有互相垂直正交的匀强电场与匀强磁场，其磁感应强度
=0.5T。一质量m=l×
kg，电荷量
的带正电的粒子以速度
从x轴上的N点沿与x轴负方向成
角方向射入第一象限，经P点进入第二象限内沿直线运动，一段时间后，粒子经x轴上的M点并与x轴负方向成角的方向飞出，M点坐标为(-0.1，0),N点坐标(0.3，0)，不计粒子重力。求:
(1)匀强电场的电场强度E的大小与方向;
(2)匀强磁场的磁感应强度的大小;
(3)匀强磁场矩形区城的最小面积。
kg的木块A套在水平杆上，并用轻绳将木块A与质量m=
kg的小球相连。今用跟水平方向成α=300角的力F=
N,拉着球带动木块一起向右匀速运动，运动中M、m相对位置保持不变，取g=10m/s2。求：
粤公网安备 44130202000953号