如图所示,一固定在竖直平面内的光滑的半圆形轨道ABC,其半径R=0.4m,轨道在C处与水平地面相切。在C处放一小物块,质量2kg,给它一水平向左的初速度v0=6m/s,结果它沿CBA运动,通过A点,最后落在水平面上 的D点,取重力加速度g=10m/s2。 求:
的D点,取重力加速度g=10m/s2。 求: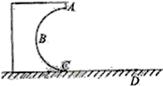
(1)小球运动到A点时的瞬时速度为多大?此时小球对轨道的弹力为?
(2)C、D间的距离L
如图所示,一固定在竖直平面内的光滑的半圆形轨道ABC,其半径R=0.4m,轨道在C处与水平地面相切。在C处放一小物块,质量2kg,给它一水平向左的初速度v0=6m/s,结果它沿CBA运动,通过A点,最后落在水平面上 的D点,取重力加速度g=10m/s2。 求:
的D点,取重力加速度g=10m/s2。 求:
(1)小球运动到A点时的瞬时速度为多大?此时小球对轨道的弹力为?
(2)C、D间的距离L