如图所示,质量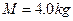 ,长
,长 的木板B静止在光滑水平地面上,其上表面正中央放置一个质量
的木板B静止在光滑水平地面上,其上表面正中央放置一个质量 的小滑块A,A与B之间的动摩擦因数为
的小滑块A,A与B之间的动摩擦因数为 。现同时给A、B瞬时冲量使二者获得水平向右的初速度,
。现同时给A、B瞬时冲量使二者获得水平向右的初速度, 、
、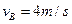 ;已知在B与墙壁碰撞前A没有滑离B,且A、B已经达到共同速度。设B与墙壁碰撞时间极短,且无机械能损失,重力加速度
;已知在B与墙壁碰撞前A没有滑离B,且A、B已经达到共同速度。设B与墙壁碰撞时间极短,且无机械能损失,重力加速度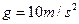 。求:
。求:
(1)B与墙壁碰撞前,A、B的共同速度大小;
(2)在B与墙壁碰撞前的过程中,A相对于B滑行的距离;
(3)A在B上滑动的整个过程中,A、B系统因摩擦产生的热量。
如图所示,质量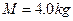 ,长
,长 的木板B静止在光滑水平地面上,其上表面正中央放置一个质量
的木板B静止在光滑水平地面上,其上表面正中央放置一个质量 的小滑块A,A与B之间的动摩擦因数为
的小滑块A,A与B之间的动摩擦因数为 。现同时给A、B瞬时冲量使二者获得水平向右的初速度,
。现同时给A、B瞬时冲量使二者获得水平向右的初速度, 、
、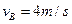 ;已知在B与墙壁碰撞前A没有滑离B,且A、B已经达到共同速度。设B与墙壁碰撞时间极短,且无机械能损失,重力加速度
;已知在B与墙壁碰撞前A没有滑离B,且A、B已经达到共同速度。设B与墙壁碰撞时间极短,且无机械能损失,重力加速度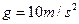 。求:
。求:
(1)B与墙壁碰撞前,A、B的共同速度大小;
(2)在B与墙壁碰撞前的过程中,A相对于B滑行的距离;
(3)A在B上滑动的整个过程中,A、B系统因摩擦产生的热量。