如图所示,在小车的右端高h=0.20m的支架上固定着一个半径为R的1/4圆弧光滑导轨,一质量为研= 0.2kg的物体从圆弧的顶端无摩擦地滑下,离开圆弧后刚好落到车的左端边沿,车与支架的总质量M=2kg,车身长L=0.22m,车与水平地面间的摩擦不计,重力加速度g =10m/s2,求:
(1) 小球离开圆弧轨道下降高度h.所用的时间;
(2) 小球滑到圆弧底端时小球和车的速度大小;
(3) 圆弧半径R。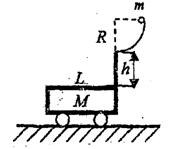
如图所示,在小车的右端高h=0.20m的支架上固定着一个半径为R的1/4圆弧光滑导轨,一质量为研= 0.2kg的物体从圆弧的顶端无摩擦地滑下,离开圆弧后刚好落到车的左端边沿,车与支架的总质量M=2kg,车身长L=0.22m,车与水平地面间的摩擦不计,重力加速度g =10m/s2,求:
(1) 小球离开圆弧轨道下降高度h.所用的时间;
(2) 小球滑到圆弧底端时小球和车的速度大小;
(3) 圆弧半径R。