如图,质量为m的b球用长h的细绳悬挂于水平轨道BC的出口C处。质量也为m的小球a,从距BC高h的A处由静止释放,沿ABC光滑轨道滑下,在C处与b球正碰并与b粘在一起。已知BC轨道距地面有一定的高度,悬挂b球的细绳能承受的最大拉力为2.8mg。试问:
①a与b球碰前瞬间的速度多大?
②a、b两球碰后,细绳是否会断裂?(要求通过计算回答)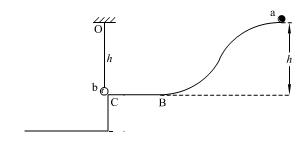
如图,质量为m的b球用长h的细绳悬挂于水平轨道BC的出口C处。质量也为m的小球a,从距BC高h的A处由静止释放,沿ABC光滑轨道滑下,在C处与b球正碰并与b粘在一起。已知BC轨道距地面有一定的高度,悬挂b球的细绳能承受的最大拉力为2.8mg。试问:
①a与b球碰前瞬间的速度多大?
②a、b两球碰后,细绳是否会断裂?(要求通过计算回答)