如图所示,静止在水平面的纸带上放一质量为m的小金属块(可视为质点),金属块离纸带右端距离为L,金属块与纸带间的动摩擦因数为μ,现用力向左将纸带从金属块下水平抽出,设纸带加速过程极短,可以认为纸带在抽动过程中一直做匀速运动,
求:(1)金属块刚开始运动时受到的 摩擦力的大小和方向;
摩擦力的大小和方向;
(2)要将纸带从金属块下水平抽出,纸带的速度v应满足的条件.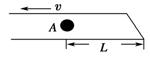
如图所示,静止在水平面的纸带上放一质量为m的小金属块(可视为质点),金属块离纸带右端距离为L,金属块与纸带间的动摩擦因数为μ,现用力向左将纸带从金属块下水平抽出,设纸带加速过程极短,可以认为纸带在抽动过程中一直做匀速运动,
求:(1)金属块刚开始运动时受到的 摩擦力的大小和方向;
摩擦力的大小和方向;
(2)要将纸带从金属块下水平抽出,纸带的速度v应满足的条件.