如图所示,竖直平行导轨间距l=20cm,导轨顶端接有一电键K。导体棒ab与导轨接触良好且无摩擦,ab的电阻R=0.4Ω,质量m=10g,导轨的电阻不计,整个装置处在与轨道平面垂直的匀强磁场中,磁感强度B=1T。当ab棒由静止释放0.8 s后,突然接通电键,不计空气阻力,设导轨足够长。求:
(1)ab棒的最大速度
(2)ab棒的最终速度的大小(g取10m/s2)。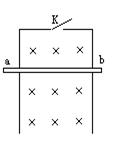
如图所示,竖直平行导轨间距l=20cm,导轨顶端接有一电键K。导体棒ab与导轨接触良好且无摩擦,ab的电阻R=0.4Ω,质量m=10g,导轨的电阻不计,整个装置处在与轨道平面垂直的匀强磁场中,磁感强度B=1T。当ab棒由静止释放0.8 s后,突然接通电键,不计空气阻力,设导轨足够长。求:
(1)ab棒的最大速度
(2)ab棒的最终速度的大小(g取10m/s2)。