如图16所示,足够长的光滑水平面上,轻弹簧两端分别拴住质量均为m 的小物块A 和B ,B物块靠着竖直墙壁。今用水平外力缓慢推A ,使A 、B间弹簧压缩,当压缩到弹簧的弹性势能为E时撤去此水平外力,让A和B在水平面上运动。
求:
⑴ 当B刚离开墙壁时,A物块的速度大小;
⑵ 当弹簧达到最大长度时A、B的速度大小;
⑶ 当B离开墙壁以后的运动过程中,弹簧弹性势能的最大值.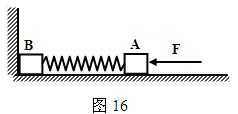
如图16所示,足够长的光滑水平面上,轻弹簧两端分别拴住质量均为m 的小物块A 和B ,B物块靠着竖直墙壁。今用水平外力缓慢推A ,使A 、B间弹簧压缩,当压缩到弹簧的弹性势能为E时撤去此水平外力,让A和B在水平面上运动。
求:
⑴ 当B刚离开墙壁时,A物块的速度大小;
⑵ 当弹簧达到最大长度时A、B的速度大小;
⑶ 当B离开墙壁以后的运动过程中,弹簧弹性势能的最大值.