如图所示,在倾角为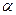 的光滑斜面上,垂直纸面放置一根长为
的光滑斜面上,垂直纸面放置一根长为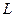 、质量为
、质量为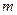 的直导体棒,当导体棒中通以垂直于纸面向里的电流
的直导体棒,当导体棒中通以垂直于纸面向里的电流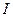 并置于竖直向上的匀强磁场中时,导体棒恰好能静止在斜面上,试求该磁场的磁感应强度是多大?如果要保持导体棒在斜面上静止且要所加磁场的磁感应强度最小,则所加磁场的方向应该怎样?最小的磁感应强度多大?
并置于竖直向上的匀强磁场中时,导体棒恰好能静止在斜面上,试求该磁场的磁感应强度是多大?如果要保持导体棒在斜面上静止且要所加磁场的磁感应强度最小,则所加磁场的方向应该怎样?最小的磁感应强度多大?
如图所示,在倾角为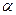 的光滑斜面上,垂直纸面放置一根长为
的光滑斜面上,垂直纸面放置一根长为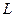 、质量为
、质量为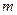 的直导体棒,当导体棒中通以垂直于纸面向里的电流
的直导体棒,当导体棒中通以垂直于纸面向里的电流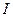 并置于竖直向上的匀强磁场中时,导体棒恰好能静止在斜面上,试求该磁场的磁感应强度是多大?如果要保持导体棒在斜面上静止且要所加磁场的磁感应强度最小,则所加磁场的方向应该怎样?最小的磁感应强度多大?
并置于竖直向上的匀强磁场中时,导体棒恰好能静止在斜面上,试求该磁场的磁感应强度是多大?如果要保持导体棒在斜面上静止且要所加磁场的磁感应强度最小,则所加磁场的方向应该怎样?最小的磁感应强度多大?