某同学的家住在一座30层的高楼内,他每天乘电梯上楼,经过多次仔细观察和反复测量,他发现电梯启动后向上运动的速度符合如下图所示的规律,他就根据这一特点在电梯内用台秤、重物和秒表测量这一楼房的高度。他将台秤放在电梯内,将重物放在台秤的托盘,电梯从第一层开始启动,经过不间断地运行,最后停在第30楼。他测得在第9.5s时台秤的示数为60N,g=10m/s2。求:
(1)电梯启动后在上升过程中台秤的最大示数;
(2)该幢楼房每一层的平均高度(结果保留3位有效数字)。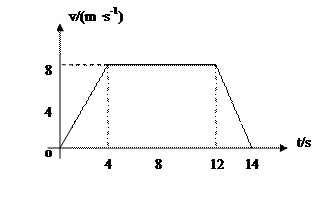
某同学的家住在一座30层的高楼内,他每天乘电梯上楼,经过多次仔细观察和反复测量,他发现电梯启动后向上运动的速度符合如下图所示的规律,他就根据这一特点在电梯内用台秤、重物和秒表测量这一楼房的高度。他将台秤放在电梯内,将重物放在台秤的托盘,电梯从第一层开始启动,经过不间断地运行,最后停在第30楼。他测得在第9.5s时台秤的示数为60N,g=10m/s2。求:
(1)电梯启动后在上升过程中台秤的最大示数;
(2)该幢楼房每一层的平均高度(结果保留3位有效数字)。