如图所示,在E=103V/m的竖直匀强电场中,有一光滑的半圆形绝缘轨道QPN与一水平绝缘轨道MN连接,半圆形轨道平面与电场线平行,P为QN圆弧的中点,其半径R=0.4m,一带正电q=10-4C的小滑块质量m=0.01kg,与水平轨道间的动摩擦因数μ=0.15,位于N 点右侧1.5m处,要使小滑块恰能运动到圆轨道的最高点Q,则滑块应以多大的初速度v0向左运动?取g=10m/s2,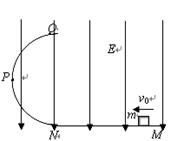
相关知识点
如图所示,在E=103V/m的竖直匀强电场中,有一光滑的半圆形绝缘轨道QPN与一水平绝缘轨道MN连接,半圆形轨道平面与电场线平行,P为QN圆弧的中点,其半径R=0.4m,一带正电q=10-4C的小滑块质量m=0.01kg,与水平轨道间的动摩擦因数μ=0.15,位于N 点右侧1.5m处,要使小滑块恰能运动到圆轨道的最高点Q,则滑块应以多大的初速度v0向左运动?取g=10m/s2,