如图所示,一带电荷量为+q、质量为m的小物块处于一倾角为37°的光滑斜面上,当整个装置被置于一水平向右的匀强电场中,小物块恰好静止。重力加速度取g, 。求:
。求:
(1)水平向右电场的电场强度;
(2)若将电场强度减小为原来的1/2,物块的加速度是多大;
(3)电场强度变化后物块下滑的距离L时的动能。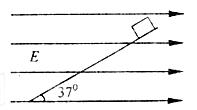
如图所示,一带电荷量为+q、质量为m的小物块处于一倾角为37°的光滑斜面上,当整个装置被置于一水平向右的匀强电场中,小物块恰好静止。重力加速度取g, 。求:
。求:
(1)水平向右电场的电场强度;
(2)若将电场强度减小为原来的1/2,物块的加速度是多大;
(3)电场强度变化后物块下滑的距离L时的动能。