电磁炮是一种理想的兵器,它的主要原理如图所示,1982年某大学的实验室制成了能把0.2 kg的弹体(包括金属杆EF的质量)经长为50 m距离加速到速度为200m/s的电磁炮,若轨道宽2m,通过的电流为10 A,(轨道的摩擦忽略不计)
求(1)在平面图中画出电磁炮受力分析图
(2)轨道间所加匀强磁场的磁感应强度为多少?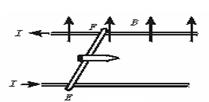
电磁炮是一种理想的兵器,它的主要原理如图所示,1982年某大学的实验室制成了能把0.2 kg的弹体(包括金属杆EF的质量)经长为50 m距离加速到速度为200m/s的电磁炮,若轨道宽2m,通过的电流为10 A,(轨道的摩擦忽略不计)
求(1)在平面图中画出电磁炮受力分析图
(2)轨道间所加匀强磁场的磁感应强度为多少?