如图a是研究小球在斜面上平抛运动的实验装置，每次将小球从弧型轨道同一位置静止释放，并逐渐改变斜面与水平地面之间的夹角θ，获得不同的射程x，最后作出了如图b所示的x-tanθ图象，g取l0m／s2，则：
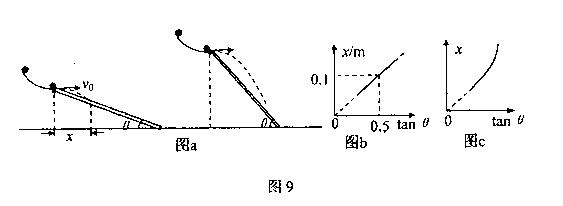
（1）由图b可知，小球在斜面顶端水平抛出时的初速度
。实验中发现θ超过60°后，小球将不会掉落在斜面上，则斜面的长度为 m。（保留1位有效数字）
（2）若最后得到的图象如图c所示，则可能的原因是 （写出一个）
如图1所示，宽度为的竖直狭长区域内（边界为
），存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场（如图2所示），电场强度的大小为
，
表示电场方向竖直向上。
时，一带正电、质量为
的微粒从左边界上的
点以水平速度
射入该区域，沿直线运动到
点后，做一次完整的圆周运动，再沿直线运动到右边界上的
点。
为线段
的中点，重力加速度为
。上述
为已知量。
(1)求微粒所带电荷量和磁感应强度
的大小；
(2)求电场变化的周期；
(3)改变宽度，使微粒仍能按上述运动过程通过相应宽度的区域，求
的最小值。
雨滴在穿过云层的过程中，不断与漂浮在云层中的小水珠相遇并结合为一体，其质量逐渐增大。现将上述过程简化为沿竖直方向的一系列碰撞。已知雨滴的初始质量为，初速度为
，下降距离l后与静止的小水珠碰撞且合并，质量变为
。此后每经过同
样的距离后，雨滴均与静止的小水珠碰撞且合并，质量依次变为
、
……
……（设各质量为已知量）。不计空气阻力。
（1）若不计重力，求第n次碰撞后雨滴的速度；
（2）若考虑重力的影响，
a.求第1次碰撞前、后雨滴的速度和
；
b.求第n次碰撞后雨滴的动能
；
利用霍尔效应制作的霍尔元件以及传感器，广泛应用于测量和自动控制等领域。
如图1，将一金属或半导体薄片垂直置于磁场中，在薄片的两个侧面
间通以电流I时，另外两侧
间产生电势差，这一现象称为霍尔效应。其原因是薄片中的移动电荷受洛伦兹力的作用向一侧偏转和积累，于是
间建立起电场
，同时产生霍尔电势差
。当电荷所受的电场力与洛伦兹力处处相等时，
和
达到稳定值，
的大小与
和
以及霍尔元件厚度
之间满足关系式
＝
，其中比例系数称为霍尔系数，仅与材料性质有关。
（1）设半导体薄片的宽度（间距）为
，请写出
和
的关系式;若半导体材料是电子导电的，请判断图1中
哪端的电势高;[
（2）已知半导体薄片内单位体积中导电的电子数为，电子的电荷量为
，请导出霍尔系数
的表达式。（通过横截面积
的电流
，其中
是导电电子定向移动的平均速率）;
（3）图2是霍尔测速仪的示意图，将非磁性圆盘固定在转轴上，圆盘的周边等距离地嵌装着个永磁体，相邻永磁体的极性相反。霍尔元件置于被测圆盘的边缘附近。当圆盘匀速转动时，霍尔元件输出的电压脉冲信号图像如图3所示。
a.若在时间内，霍尔元件输出的脉冲数目为
，请导出圆盘转速N的表达式。
b.利用霍尔测速仪可以测量汽车行驶的里程。除此之外，请你展开"智慧的翅膀"，提出另一个实例或设想。
如图，跳台滑雪运动员经过一段加速滑
行后从点水平飞出，经过3.0
落到斜坡上的A点。已知
点是斜坡的起点，斜坡与水平面的夹角
＝37°，运动员的质量
＝50
。不计空气阻力。（取
37°＝0.60，
37°＝0.80;
取10
）求
（1）点与
点的距离
;
（2）运动员离开点时的速度大小;
（3）运动员落到点时的动能。
粤公网安备 44130202000953号