如图为古代战争中使用的抛石机示意图,挡板P垂直固定在长木杆上,长木杆可以绕固定轴O在竖直平面内转动,现从图示位置在长木杆一端施加力F,使石块获得一定的初速度后抛出去。如果长木杆在与水平地面成37°角瞬间,石块被抛了出去,上抛到 最高点时恰好在离抛出点高度为H=20m的城墙上,则:(抛出后空气的阻力忽略不计,重力加速度取10m/s2)
最高点时恰好在离抛出点高度为H=20m的城墙上,则:(抛出后空气的阻力忽略不计,重力加速度取10m/s2)
(1)抛出瞬间石块的初 速度多大?
速度多大?
(2)抛出点与城墙的水平距离多远?
(3)抛石机的效率为50%,石块的M=50kg,抛动过程中拉力至少要做多少功?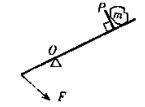
如图为古代战争中使用的抛石机示意图,挡板P垂直固定在长木杆上,长木杆可以绕固定轴O在竖直平面内转动,现从图示位置在长木杆一端施加力F,使石块获得一定的初速度后抛出去。如果长木杆在与水平地面成37°角瞬间,石块被抛了出去,上抛到 最高点时恰好在离抛出点高度为H=20m的城墙上,则:(抛出后空气的阻力忽略不计,重力加速度取10m/s2)
最高点时恰好在离抛出点高度为H=20m的城墙上,则:(抛出后空气的阻力忽略不计,重力加速度取10m/s2)
(1)抛出瞬间石块的初 速度多大?
速度多大?
(2)抛出点与城墙的水平距离多远?
(3)抛石机的效率为50%,石块的M=50kg,抛动过程中拉力至少要做多少功?