已知氢原子处于基态时,原子的能量E1=-13.6 eV,电子的轨道半径为r1=0.53×10-10 m;而量子数为n的能级值为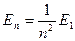 ,半径
,半径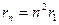 .试问(结果保留两位有效数字):
.试问(结果保留两位有效数字):
(1)若要使处于n=2的激发态的氢原子电离,至少要用频率多大的光照射氢原子?
(2)氢原子处于n=2能级时,电子在轨道上运动的动能和电子的电势能各为多少?
(静电力常量k=9×109 N·m2/C2,电子电荷量e=1.6×10-19 C,普朗克常量h=6.63× 10-34 J·s)
10-34 J·s)
已知氢原子处于基态时,原子的能量E1=-13.6 eV,电子的轨道半径为r1=0.53×10-10 m;而量子数为n的能级值为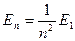 ,半径
,半径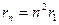 .试问(结果保留两位有效数字):
.试问(结果保留两位有效数字):
(1)若要使处于n=2的激发态的氢原子电离,至少要用频率多大的光照射氢原子?
(2)氢原子处于n=2能级时,电子在轨道上运动的动能和电子的电势能各为多少?
(静电力常量k=9×109 N·m2/C2,电子电荷量e=1.6×10-19 C,普朗克常量h=6.63× 10-34 J·s)
10-34 J·s)