在竖直面内有一光滑水平直轨道和一光滑半圆形轨道,二者在半圆的一个端点B相切,如图所示,半圆形轨道的另一端点为C,半径为R。在直轨道上距离B为x的A点,有一可看作质点的质量为m的小球处于静止状态。现用水平恒力将小球推到B处后撤去恒力,小球沿半圆轨道运动到C处后又落到水平面上。求: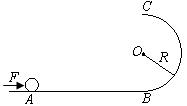
(1)若小球正好落到出发点A处,在这种情况下:
①用x和给出的已知量来表达推力对小球所做的功;
②x取何值时,水平恒力做功最小?最小值为多少?
(2)在任意情况下,x取任意值,求小球在B处和C处对轨道的压力大小之差?
在竖直面内有一光滑水平直轨道和一光滑半圆形轨道,二者在半圆的一个端点B相切,如图所示,半圆形轨道的另一端点为C,半径为R。在直轨道上距离B为x的A点,有一可看作质点的质量为m的小球处于静止状态。现用水平恒力将小球推到B处后撤去恒力,小球沿半圆轨道运动到C处后又落到水平面上。求: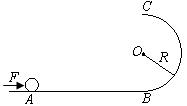
(1)若小球正好落到出发点A处,在这种情况下:
①用x和给出的已知量来表达推力对小球所做的功;
②x取何值时,水平恒力做功最小?最小值为多少?
(2)在任意情况下,x取任意值,求小球在B处和C处对轨道的压力大小之差?