地球质量为M,半径为R,自转角速度为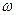 ,万有引力恒量为G,若规定物体离无穷远处势能为0,则质量为
,万有引力恒量为G,若规定物体离无穷远处势能为0,则质量为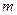 的物体离地心距离为
的物体离地心距离为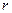 时,具有的引力势能可表示为
时,具有的引力势能可表示为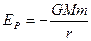 。
。
(1)试证明一质量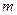 的卫星在离地面距离为
的卫星在离地面距离为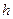 时所具有的机械能为
时所具有的机械能为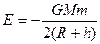
(2)国际空间站是在地球大气层上空绕地球飞行的一个巨大人造天体,设空间站离地面高度为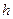 ,如果在该空间站直接发射一颗质量为
,如果在该空间站直接发射一颗质量为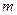 的小卫星,使其能达到地球同步卫星轨道并能在轨道上正常运行,该卫星在离开空间站时必须具有多大的初动能。
的小卫星,使其能达到地球同步卫星轨道并能在轨道上正常运行,该卫星在离开空间站时必须具有多大的初动能。
地球质量为M,半径为R,自转角速度为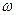 ,万有引力恒量为G,若规定物体离无穷远处势能为0,则质量为
,万有引力恒量为G,若规定物体离无穷远处势能为0,则质量为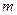 的物体离地心距离为
的物体离地心距离为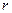 时,具有的引力势能可表示为
时,具有的引力势能可表示为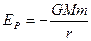 。
。
(1)试证明一质量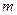 的卫星在离地面距离为
的卫星在离地面距离为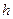 时所具有的机械能为
时所具有的机械能为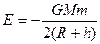
(2)国际空间站是在地球大气层上空绕地球飞行的一个巨大人造天体,设空间站离地面高度为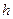 ,如果在该空间站直接发射一颗质量为
,如果在该空间站直接发射一颗质量为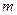 的小卫星,使其能达到地球同步卫星轨道并能在轨道上正常运行,该卫星在离开空间站时必须具有多大的初动能。
的小卫星,使其能达到地球同步卫星轨道并能在轨道上正常运行,该卫星在离开空间站时必须具有多大的初动能。