如图所示电路，U恒为10V、R1=4Ω、R2=6Ω、C1=C2=30μF，先闭合开关S，待电路稳定后再断开S，求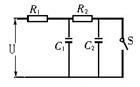
（1）闭合开关S稳定后，C1上的电量；
（2）断开开关S稳定后，C2上的电量
（3）从闭合S稳定到断开S稳定过程中,通过电阻R2、R1的电荷量.
如图所示，在高出水平地面
的光滑平台上放置一质量
、由两种不同材料连接成一体的薄板A，其右段长度
且表面光滑，左段表面粗糙。在A最右端放有可视为质点的物块B，其质量
。B与A左段间动摩擦因数
。开始时二者均静止，先对A施加
水平向右的恒力，待B脱离A（A尚未露出平台）后，将A取走。B离开平台后的落地点与平台右边缘的水平距离
。（取
）求：
（1）B离开平台时的速度
。
（2）B从开始运动到刚脱离A时，B运动的时间
和位移xB
（3）A左端的长度l2
如图所示，在光滑的桌面上叠放着一质量为mA="2.0" kg的薄木板A和质量为mB="3" kg的金属块B.A的长度L="2.0" m.B上有轻线绕过定滑轮与质量为mC="1.0" kg的物块C相连.B与A之间的动摩擦因数μ=0.10，最大静摩擦力可视为等于滑动摩擦力.忽略滑轮质量及与轴间的摩擦.起始时令各物体都处于静止状态，绳被拉直，B位于A的左端(如图)，然后放手，求经过多长时间后B从 A的右端脱离(设 A的右端距滑轮足够远)(取g="10" m/s2).
如图所示，高为h的车厢在平直轨道上匀减速向右行驶，加速度大小为a，车厢顶部A点处有油滴滴落到车厢地板上，车厢地板上的O点位于A点的正下方，则油滴落地点必在O点的左方还是右方？离O点距离为多少？
如图所示，在台秤上放半杯水，台秤示数为G′＝50 N，另用挂在支架上的弹簧测力计悬挂一边长a＝10 cm的金属块，金属块的密度ρ＝13×103 kg/m3，当把弹簧测力计下的金属块平稳地浸入水深b＝4 cm时，弹簧测力计和台秤的示数分别为多少？(水的密度是ρ水＝103 kg/m3，g取10 m/s2)
粤公网安备 44130202000953号