(14分)如图所示,一个质量为m,带电荷量为+q的粒子在O点以v0的初速度跟水平方向成α角向上射出,如果在某方向上加上一定大小的匀强电场后,可使粒子沿初速度所在直线方向做直线运动。已知重力加速度为g.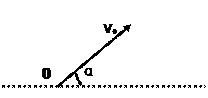
(1)若粒子做匀速直线运动则场强的大小和方向;
(2)求所加最小匀强电场的场强的大小;
(3)若加上水平向左、大小一定的匀强电场后,经过一段时间粒子又回到了O点,求粒子回到O点时的速度大小v和所用的时间t。
(14分)如图所示,一个质量为m,带电荷量为+q的粒子在O点以v0的初速度跟水平方向成α角向上射出,如果在某方向上加上一定大小的匀强电场后,可使粒子沿初速度所在直线方向做直线运动。已知重力加速度为g.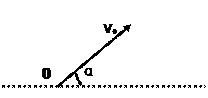
(1)若粒子做匀速直线运动则场强的大小和方向;
(2)求所加最小匀强电场的场强的大小;
(3)若加上水平向左、大小一定的匀强电场后,经过一段时间粒子又回到了O点,求粒子回到O点时的速度大小v和所用的时间t。