在2008年北京奥运会中郭晶晶获得女子个人3米板跳水冠军，其跳水的过程可简化为：运动员将跳板向下压到最低点C，跳板反弹将运动员上抛到最高点A，然后做自由落体运动，竖直落入水中。如果将运动员视为质点，且已知运动员的质量为m，重力加速度为g，AB间、BC间和B与水面间的竖直距离分别为h1、h2、h3，如图所示。试求：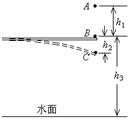
（1）运动员从A点下落到水面的时间和她入水时的速度大小；
（2）跳板反弹过程中对运动员所做的功W。
相关试题
一个质量m= 6kg的物体，初速度v0=2m/s,受到水平方向的拉力F=10N，如图所示，在水平地面上移动的距离L=2m，物体与地面间的滑动摩擦力f= 4N，求：
（1）拉力和摩擦力对物体所做的功；
（2）合外力对物体所做的功；
（3）在此过程中物体获得的速度大小。
如图，质量m=50kg的跳水运动员从距水面高h=10m的跳台上以v0=5m/s的速度斜向上起跳，最终落入水中。若忽略运动员的身高。取g=10m/s2。
求：（1）运动员在跳台上时的重力势能（以水面为参考平面）；
（2）运动员起跳时的动能；
（3）运动员入水时的速度大小。
一质量为4kg的小球从空中做自由落体运动，取g=10m/s2，求物体：（1）前2s内重力对物体做的功；（2）前2s内重力的平均功率；（3）第2s末重力的瞬时功率。
。求：
； 
粤公网安备 44130202000953号