如图所示,位于竖直平面内的光滑轨道,由一段斜的直轨道和与之相切的圆形轨道连
接而成,圆形轨道得半径为R.一质量为m的小物块从斜轨道上某处由静止开始下滑,然
后沿圆形轨道运动.要求物块能通过圆形轨道最高点,且在该最高点与轨道间的压力不能
超过5mg(g为重力加速度),求物块初始位置相对于圆形轨道底部的高度h的取值范围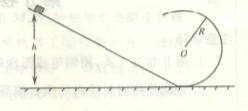
如图所示,位于竖直平面内的光滑轨道,由一段斜的直轨道和与之相切的圆形轨道连
接而成,圆形轨道得半径为R.一质量为m的小物块从斜轨道上某处由静止开始下滑,然
后沿圆形轨道运动.要求物块能通过圆形轨道最高点,且在该最高点与轨道间的压力不能
超过5mg(g为重力加速度),求物块初始位置相对于圆形轨道底部的高度h的取值范围