如图所示，匀强磁场的磁感应强度B=0.5T，边长为L=10cm的正方形线圈
abcd共100匝，线圈总电阻r=1Ω，线圈绕垂直于磁感线的对称轴OO’匀速转动，角速度
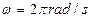，外电路电阻R=4Ω，求：
（1）转动过程中感应电动势的最大值；
（2）由图示位置（线圈平面与磁感线平行）转过60º角时的瞬时感应电动势；[
（3）交变电压表的示数；
（4）线圈转动一周外力所做的功；
（5）周期内通过R的
电荷量为多少？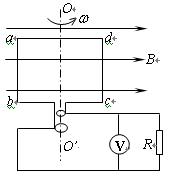
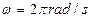如图所示，匀强磁场的磁感应强度B=0.5T，边长为L=10cm的正方形线圈abcd共100匝，线圈总电阻r=1Ω，线圈绕垂直于磁感线的对称轴OO’匀速转动，角速度，外电路电阻R=4Ω，求：
（1）转动过程中感应电动势的最大值；
（2）由图示位置（线圈平面与磁感线平行）转过60º角时的瞬时感应电动势；[
（3）交变电压表的示数；
（4）线圈转动一周外力所做的功；
（5）周期内通过R的电荷量为多少？
粤公网安备 44130202000953号