如图所示,在磁感应强度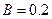 T的水平匀强磁场中,有一边长为L=10cm,匝数N=100匝,电阻r=1Ω的正方形线圈绕垂直于磁感线的
T的水平匀强磁场中,有一边长为L=10cm,匝数N=100匝,电阻r=1Ω的正方形线圈绕垂直于磁感线的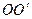 轴匀速转动,转速
轴匀速转动,转速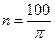 r/s,有一电阻R=9Ω,通过电刷与两滑环接触,R两端接有一理想电压表,求:
r/s,有一电阻R=9Ω,通过电刷与两滑环接触,R两端接有一理想电压表,求: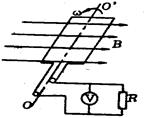
(1)若从线圈通过中性面时开始计时,写出电动势瞬时值表达式;
(2)求从中性面开始转过1/6T时的感应电动势与电压表的示数;
(3)在1分钟内外力驱动线圈转动所作的功。
相关知识点
如图所示,在磁感应强度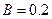 T的水平匀强磁场中,有一边长为L=10cm,匝数N=100匝,电阻r=1Ω的正方形线圈绕垂直于磁感线的
T的水平匀强磁场中,有一边长为L=10cm,匝数N=100匝,电阻r=1Ω的正方形线圈绕垂直于磁感线的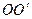 轴匀速转动,转速
轴匀速转动,转速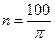 r/s,有一电阻R=9Ω,通过电刷与两滑环接触,R两端接有一理想电压表,求:
r/s,有一电阻R=9Ω,通过电刷与两滑环接触,R两端接有一理想电压表,求:
(1)若从线圈通过中性面时开始计时,写出电动势瞬时值表达式;
(2)求从中性面开始转过1/6T时的感应电动势与电压表的示数;
(3)在1分钟内外力驱动线圈转动所作的功。