.如图(甲)所示,在xoy平面内有足够大的匀强电场,电场方向竖直向上,电场强度E=40N/C.在y轴左侧平面内有足够大的瞬时磁场,磁感应强度B1随时间t变化规律如图(乙)所示,15π s后磁场消失,选定磁场垂直向里为正方向.在y轴右侧平面内还有方向垂直纸面向外的恒定的匀强磁场,分布在一个半径为r=0.3m的圆形区域(图中未画出),且圆的左侧与y轴相切,磁感应强度B2=0.8T.t=0时刻,一质量m=8×10-4kg、电荷量q=2×10-4C的微粒从x轴上xP=-0.8m处的P点以速度v=0.12m/s向x轴正方向入射.(计算结果保留二位有效数字)
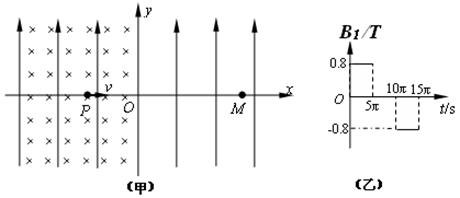
(1)求微粒在第二像限运动过程中离y轴、x轴的最大距离;
(2)若微粒穿过y轴右侧圆形磁场时,速度方向的偏转角度最大,求此圆形磁场的圆心坐标(x、y);
(3)若微粒以最大偏转角穿过磁场后, 击中x轴上的M点,求微粒从射入圆形磁场到击中M点的运动时间t。

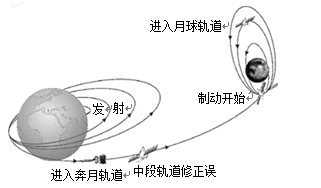
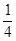 R地,g月=
R地,g月=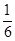 g地,则近月卫星的运行速度约为近地卫星运行速度的多少倍?
g地,则近月卫星的运行速度约为近地卫星运行速度的多少倍?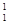 H)转化成一个氦核(
H)转化成一个氦核(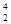 He)和两个正电子(
He)和两个正电子(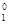 e)并放出能量.已知质子质量mP = 1.0073u,α粒子的质量mα = 4.0015u,电子的质量me = 0.0005u. 1u的质量相当于931.MeV的能量.
e)并放出能量.已知质子质量mP = 1.0073u,α粒子的质量mα = 4.0015u,电子的质量me = 0.0005u. 1u的质量相当于931.MeV的能量.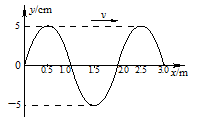
 粤公网安备 44130202000953号
粤公网安备 44130202000953号