人和雪橇的总质量为75kg,沿倾角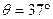 且足够长的斜坡向下运动,已知雪橇所受的空气阻力与速度成正比,比例系数k未知,从某时刻开始计时,测得雪橇运动的v-t图象如图中的曲线AD所示,图中AB是曲线在A点的切线,切线上一点B的坐标为(4,15),CD是曲线AD的渐近线,g取10m/s2,试回答和求解:
且足够长的斜坡向下运动,已知雪橇所受的空气阻力与速度成正比,比例系数k未知,从某时刻开始计时,测得雪橇运动的v-t图象如图中的曲线AD所示,图中AB是曲线在A点的切线,切线上一点B的坐标为(4,15),CD是曲线AD的渐近线,g取10m/s2,试回答和求解:
(1)雪橇在下滑过程中,开始做什么运动,最后做什么运动?
(2)当雪橇的速度为5m/s时,雪橇的加速度为多大?
(3)雪橇与斜坡间的动摩擦因数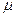 多大?
多大?
人和雪橇的总质量为75kg,沿倾角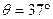 且足够长的斜坡向下运动,已知雪橇所受的空气阻力与速度成正比,比例系数k未知,从某时刻开始计时,测得雪橇运动的v-t图象如图中的曲线AD所示,图中AB是曲线在A点的切线,切线上一点B的坐标为(4,15),CD是曲线AD的渐近线,g取10m/s2,试回答和求解:
且足够长的斜坡向下运动,已知雪橇所受的空气阻力与速度成正比,比例系数k未知,从某时刻开始计时,测得雪橇运动的v-t图象如图中的曲线AD所示,图中AB是曲线在A点的切线,切线上一点B的坐标为(4,15),CD是曲线AD的渐近线,g取10m/s2,试回答和求解:
(1)雪橇在下滑过程中,开始做什么运动,最后做什么运动?
(2)当雪橇的速度为5m/s时,雪橇的加速度为多大?
(3)雪橇与斜坡间的动摩擦因数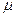 多大?
多大?