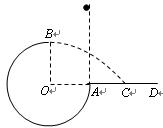
如图所示，竖直平面内的3/4圆弧形光滑轨道半径为R，A端与圆心O等高，AD为水平面，B点为光滑轨道的最高点且在O的正上方，一个小球在A点正上方由静止释放，自由下落至A点进入圆轨道并恰好能通过B点，最后落到水平面C点处。求：
（1）小球通过轨道B点的速度大小；
（2）释放点距A点的竖直高度；
（3）落点C与A点的水平距离。