一匀强磁场,磁场方向垂直于xy平面,在xy平面上,磁场分布在以O为中心的一个圆形区域内.一个质量为m、电荷量为q的带电粒子,由原点O开始运动,初速度为v,方向沿x轴正方向,后来,粒子经过y轴上的P点,此时速度方向与y轴的夹角为30°,P到O的距离为l,如图2所示.不计重力的影响,求磁场的磁感应强度B的大小和xy平面上的磁场区域的半径R.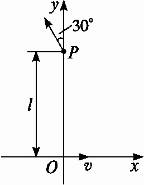
图2
相关试题
一半圆形玻璃砖，玻璃的折射率为
，AB为其直径，长度为D，O为圆心.一束宽度恰等于玻璃砖半径的单色平行光束垂直于AB从空气射入玻璃砖，其中心光线P通过O点，如图19-2-17所示.M、N为光束边界光线.则M、N射出玻璃砖后的相交点距O点的距离为多少？
图19-2-17
在折射率为n、厚度为d的玻璃平板上方的空气中有一点光源S，从S发出的光线SA以角度θ入射到玻璃板上表面，经过玻璃板后从下表面射出，如下图所示.若沿此光线传播的光从光源到玻璃板上表面的传播时间与在玻璃板中的传播时间相等，点光源S到玻璃板上表面的垂直距离L应是多少?
一束光线射到一个玻璃球上，如图19-2-10所示，该玻璃圆球的折射率是
，光线的入射角是60°.求该束光线射入玻璃球后第一次从玻璃球射出的方向.
图19-2-10
粤公网安备 44130202000953号